Next: `View' menu Up: Reference Function List (by Previous: `Edit' menu
- Size
 Half Size (Quick/simple)
M
Half Size (Quick/simple)
M
- Size
 Half Size (Slower/accurate)
M
Half Size (Slower/accurate)
M
- Size
 Double Size
M
Double Size
M
- Size
 Half Size X
M
Half Size X
M
- Size
 Half Size Y
M
Half Size Y
M
- Size
 Arbitrary Resize...
M
Arbitrary Resize...
M
- Planar Transformations
 Rotate
Rotate 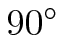 [R]
M
[R]
M
- Planar Transformations
 Rotate
Rotate 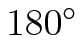 M
M
- Planar Transformations
 Rotate
Rotate 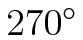 [Shift+R]
M
[Shift+R]
M
- Planar Transformations
 Rotate Arbitrary...
M
Rotate Arbitrary...
M
- Planar Transformations
 Flip Horizontal [H]
M
Flip Horizontal [H]
M
- Planar Transformations
 Flip Vertical [V]
M
Flip Vertical [V]
M
- Planar Transformations
 Shift with Wrap...
M
Shift with Wrap...
M
- Planar Transformations
 Shear...
M
Shear...
M
- Planar Transformations
 Rectify...
M
Rectify...
M
- Spherical Transformations
 Panoramic Transformations...
Panoramic Transformations...
- Spherical Transformations
 Diffuse/Specular Convolution...
M
Diffuse/Specular Convolution...
M
- Spherical Transformations
 Ward Specular Convolution...
M
Ward Specular Convolution...
M
- Spherical Transformations
 Fast Diffuse Convolution (Lat-Long)
M
Fast Diffuse Convolution (Lat-Long)
M
- Spherical Transformations
 Spherical Harmonic Reconstruct Lat-Long...
M
Spherical Harmonic Reconstruct Lat-Long...
M
- Spherical Transformations
 Sample Light Probe Image to Light Source List...
M
Sample Light Probe Image to Light Source List...
M
- Filter
 Neighbor Average Blur
M
Neighbor Average Blur
M
- Filter
 Gaussian Blur...
M
Gaussian Blur...
M
- Filter
 Bilateral Filter...
M
Bilateral Filter...
M
- Filter
 Motion Blur...
M
Motion Blur...
M
- Filter
 Horizontal Motion Blur...
M
Horizontal Motion Blur...
M
- Filter
 Circle Blur...
M
Circle Blur...
M
- Filter
 Small Circle Blur...
M
Small Circle Blur...
M
- Filter
 Star Filter
M
Star Filter
M
- Filter
 Deinterlace
M
Deinterlace
M
- Filter
 Incremental Adaptive Unsharp Sharpen [^]
M
Incremental Adaptive Unsharp Sharpen [^]
M
- Filter
 Sharpen By... [Ctrl+6]
M
Sharpen By... [Ctrl+6]
M
- Filter
 Laplacian of Gaussian...
M
Laplacian of Gaussian...
M
- Filter
 X Derivative
M
X Derivative
M
- Filter
 Y Derivative
M
Y Derivative
M
- Filter
 Gradient
M
Gradient
M
- Filter
 Corner Detect
M
Corner Detect
M
- Filter
 Edge Detectors
Edge Detectors Gradient Based...
M
Gradient Based...
M
- Filter
 Edge Detectors
Edge Detectors Laplacian of Gaussian Based...
M
Laplacian of Gaussian Based...
M
- Filter
 Calculate Normals
M
Calculate Normals
M
- Filter
 Interpolate Bayer Pattern...
M
Interpolate Bayer Pattern...
M
- Filter
 DCT (Discrete Cosine Transform)
M
DCT (Discrete Cosine Transform)
M
- Filter
 IDCT (Inverse Discrete Cosine Transform)
M
IDCT (Inverse Discrete Cosine Transform)
M
- Warp
 Correct Lens Distortion
M
Correct Lens Distortion
M
- Effects
 Vignette...
M
Vignette...
M
- Effects
 Randomize
M
Randomize
M
- Effects
 Sepia tone...
M
Sepia tone...
M
- Effects
 Quantize
M
Quantize
M
- Effects
 Signed Quantize
M
Signed Quantize
M
- Effects
 Vertical Cosine Falloff
M
Vertical Cosine Falloff
M
- Pixel
 Set/Clear...
M
Set/Clear...
M
- Pixel
 Offset...
M
Offset...
M
- Pixel
 Scale...
M
Scale...
M
- Pixel
 Divide...
M
Divide...
M
- Pixel
 Power...
M
Power...
M
- Pixel
 Exponentiate...
M
Exponentiate...
M
- Pixel
 Log...
M
Log...
M
- Pixel
 Replace Infinite/NAN...
M
Replace Infinite/NAN...
M
- Pixel
 Round
M
Round
M
- Pixel
 Floor
M
Floor
M
- Pixel
 Ceiling
M
Ceiling
M
- Pixel
 Desaturate
M
Desaturate
M
- Pixel
 Scale to Current Exposure [Ctrl+0]
M
Scale to Current Exposure [Ctrl+0]
M
- Pixel
 Clamp at Current Exposure
M
Clamp at Current Exposure
M
- Pixel
 Normalize
M
Normalize
M
- Pixel
 Lower Threshold...
M
Lower Threshold...
M
- Pixel
 Upper Threshold...
M
Upper Threshold...
M
- Pixel
 Swap Byte Order [B]
M
Swap Byte Order [B]
M
- Pixel
 White-Balance Selection
M
White-Balance Selection
M
- Pixel
 Scale Selection to White
M
Scale Selection to White
M
- Pixel
 Compute Color Matrix...
Compute Color Matrix...
- Pixel
 Apply Color Matrix...
M
Apply Color Matrix...
M
- Pixel
 Rasterize Triangle
M
Rasterize Triangle
M
- Pixel
 Index Map
M
Index Map
M
- Info
 Max/Min/Average [I]
Max/Min/Average [I]
- Info
 Copy Average [C]
Copy Average [C]
- Info
 Sample Grid...
Sample Grid...
- Crop M
- Calculate
- Duplicate [D]
`Image' menu
Size Half Size (Quick/simple)
M
Half Size (Quick/simple)
M
Half-size an image by dividing the image into a square grid with each square containing 4
pixels. Simply take the average value of the 4 pixels and write out as one pixel. This method
produces aliasing at boundaries of contrast in the image (cf. 10.2).
Size Half Size (Slower/accurate)
M
Half Size (Slower/accurate)
M
Half-size the image using a simple small blur kernel of size 1-2-1. This helps reduce aliasing
which may be present if the Quick/Simple method is used(10.1). The image
is blurred slightly in the horizontal direction for each consecutive 3 pixels with a 1-2-1
weighting function. This is repeated for the vertical direction, then a 'Half Size (Quick/simple)
is done on the blurred image. The resulting image is thus slightly blurred such that simple
half-size aliasing is diminished giving a less jagged result. The process is slightly
slower due to the double blur operation.
Size Double Size
M
Double Size
M
Double the width & height of the image. Uses bilinear interpolation of the existing values to
infer the extra pixel values.
Size Half Size X
M
Half Size X
M
Reduce the width of the image by half from the average of consecutive pairs of pixels in each
horizontal line in the image.
Size Half Size Y
M
Half Size Y
M
Reduce the height of the image by half from the average of consecutive pairs of pixels in each
vertical line in the image.
Size Arbitrary Resize...
M
Arbitrary Resize...
M
Change the image dimensions to any values. Choosing this item prompts the user with a dialog allowing
the dimensions to be specified along with choice of resizing method:
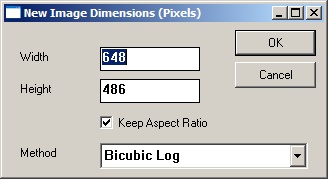
One of the following resizing methods is chosen (in order of increasing quality/decreasing speed):
- Nearest neighbor interpolation:
Pixel values from the old image are copied in to the nearest corresponding location in the new image regardless of the surrounding pixel values. - Bilinear interpolation:
Uses the 4 surrounding pixels (horizontally and vertically) to interpolate values. - Bicubic interpolation:
Uses the a weighted average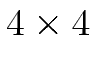 square of neighboring pixels from the original image
to drive the interpolation. Weights are derived in terms of a cubic function.
square of neighboring pixels from the original image
to drive the interpolation. Weights are derived in terms of a cubic function.
- BSpline interpolation:
Uses the a weighted average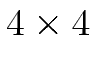 square of neighboring pixels from the original image
to drive the interpolation. Weights are derived in terms of a BSpline function.
square of neighboring pixels from the original image
to drive the interpolation. Weights are derived in terms of a BSpline function.
- Bilinear Log interpolation:
Uses the 4 surrounding pixels (horizontally and vertically) to interpolate values in Log space. - Bicubic Log interpolation [default]:
Uses the a weighted average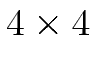 square of neighboring pixels from the original image
to drive the interpolation. Weights are derived in terms of a cubic function and in Log space.
square of neighboring pixels from the original image
to drive the interpolation. Weights are derived in terms of a cubic function and in Log space.
Planar Transformations Rotate
Rotate 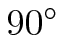 [R]
M
[R]
M
Rotate the image by
Planar Transformations Rotate
Rotate 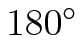 M
M
Rotate the image by
Planar Transformations Rotate
Rotate 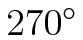 [Shift+R]
M
[Shift+R]
M
Rotate the image by
Planar Transformations Rotate Arbitrary...
M
Rotate Arbitrary...
M
Rotate the image by an arbitrary amount. The user specifies the amount of clockwise rotation
in degrees. Note: the resulting image will be larger, reflecting the rectangular bounding rectangle
that touches the rotated image corners. New pixels are set to black.
Planar Transformations Flip Horizontal [H]
M
Flip Horizontal [H]
M
Flip the image across the right vertical edge
Planar Transformations Flip Vertical [V]
M
Flip Vertical [V]
M
Flip the image across the bottom horizontal edge
Planar Transformations Shift with Wrap...
M
Shift with Wrap...
M
Shift the image up or down and left or right. Pixels that are shifted off one edge
are tacked on to the opposite edge ('wrapped').
Planar Transformations Shear...
M
Shear...
M
Shear the image so that the bottom edge moves relative to the top. The amount of shear is selected
as:
(bottom edge horizontal shift)
The resulting image will be larger than the original to accomodate the bounding rectangle which touches the sheared image corners.
Planar Transformations Rectify...
M
Rectify...
M
Resample a quadrilateral area within the image to a rectangular image with the same or different
dimensions. In order to rectify a quadrilateral area, first the area must be demarcated with 4 points
(Shift+left-click) using the 'Point Editor' window (15.12). The 4 points must be
arranged so that they form the quadrilateral when taken in anti-clockwise order beginning from the
top-leftmost location. Select 'Image
Spherical Transformations Panoramic Transformations...
Panoramic Transformations...
Transform a panoramic source image into any of several useful other panoramic image spaces.
See the online tutorials here
for more information on these formats and an example of how to create a panormaic transformation.
The source/destination panoramic spaces can be any of:
- Light Probe (Angular Map)
- Mirrored Ball
- Mirrored Ball Closeup
- Diffuse Ball
- Latitude/Longitude
- Cubic environment (Vertical Cross)
- Cubic environment (Horizontal Cross)
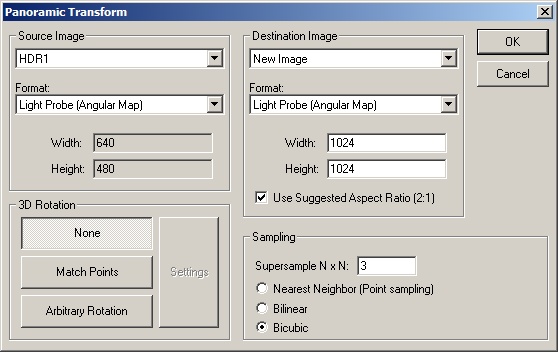
Choose the source image from the list of open images. Describe the panoramic format of the source image from the drop-down box as described above. Choose the target image or use the default behavior which is to create a new image. Choose the panoramic transformation format for the output image. Specify the output image dimensions, note the aspect ratio check box, and (optionally) specify a 3D rotation.
Spherical Transformations Diffuse/Specular Convolution...
M
Diffuse/Specular Convolution...
M
HDR Shop can perform a diffuse or specular convolution on a high-dynamic range
Spherical Transformations Ward Specular Convolution...
M
Ward Specular Convolution...
M
Simulates a rough specular sphere lit by a light probe. The input and output images should be
in lat-long format (see 10.16). Furthermore the input image must have width = 2
Spherical Transformations Fast Diffuse Convolution (Lat-Long)
M
Fast Diffuse Convolution (Lat-Long)
M
Simulates a diffuse sphere lit by a light probe. The input and output images should be
in lat-long format (see 10.16).
The output image will be a diffuse convolution of the input image or light probe using the Lambertian BRDF model.
This is useful if you need to pre-compute a diffuse texture map; for example, to light an
object using a light probe in real time applications. Lighting a diffuse surface with a preconvolved
environment map produces a similar effect to lighting an actual diffuse surface with the original light probe.
An example HDRShop script which performs the function can also be found
here
Spherical Transformations Spherical Harmonic Reconstruct Lat-Long...
M
Spherical Harmonic Reconstruct Lat-Long...
M
Approximates the input image/light probe as a sum of spherical harmonics up to the desired order. See this
here
for more information.
Spherical Transformations Sample Light Probe Image to Light Source List...
M
Sample Light Probe Image to Light Source List...
M
Samples a spherical lighting environment image into a number of areas where each area contains a single light source.
Choice of areas and light source positions and intensities are computed based on the distribution of energy in parts
of the image. In this way, the light source position and intensity most representative of each particular area is
obtained. This is useful in rendering lighting environments where efficiency is paramount and a good approximation
to the full resolution environment will suffice. The output is a text window listing the sampled positions and
intensities in one of: plain text (spherical positions in radians or degrees, or as unit vectors on the sphere), Maya MEL
script, or PBRT format, and also optionally either or both of: an image showing sampled pixel lighting
locations and intensities; an image showing the subdivision areas of the image as a graph.
The 'Sample Panoramic Lighting Environment...' dialog:
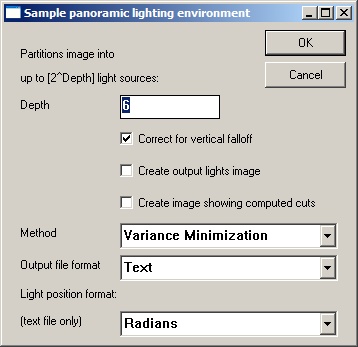
Filter Neighbor Average Blur
M
Neighbor Average Blur
M
Each pixel is set to a weighted distance average of its immediate 8 neighbors.
Performs very simple, very fast blur of fixed size.
Filter Gaussian Blur...
M
Gaussian Blur...
M
Apply a 2D Gaussian blur with specified kernel width in pixels
Filter Bilateral Filter...
M
Bilateral Filter...
M
Edge-preserving blurring filter. The filter weights the convolution in 2 domains so that
the pixel is replaced with the weighted average of its neighbors in both space and intensity.
Filter Motion Blur...
M
Motion Blur...
M
Produces a linear blur with a selected width and at a selected angle chosen from a dialog box.
Pixels are given the average value of all pixels (including subpixels) within the angled window with the given width.
Filter Horizontal Motion Blur...
M
Horizontal Motion Blur...
M
Approximates horizontal motion blur by setting each pixel to be the average of pixels in a window with width
specified in the dialog box. Optimized to be faster than motion blur with arbitrary direction.
Filter Circle Blur...
M
Circle Blur...
M
A simple blur filter which creates a circular kernel with the radius given in the dialog box. The
values within the kernel sum to 1. The image is then convolved with this kernel. The kernel format
is such that inside the circle, the values are the same everywhere and the edge pixels fall off
smoothly from this value (akin to a Gaussian blur with minimal spread).
Filter Small Circle Blur...
M
Small Circle Blur...
M
A simple blur filter which creates the following ![$ \left[ \begin{array}{ccccc}
0.000000 & 0.015873 & 0.039683 & 0.015873 & 0.0000...
...73 \\
0.000000 & 0.015873 & 0.039683 & 0.015873 & 0.000000 \end{array} \right]$](img14.gif)
to produce a weighted circular distance average value for each pixel.
Filter Star Filter
M
Star Filter
M
Generates s vertical and horizontal star-shaped blur approximating simple image glare.
Filter Deinterlace
M
Deinterlace
M
Removes common 'tearing' artifacts in deinterlaced images by doing a simple 1-2-1 weighted vertical blur on the
consecutive interlaced fields.
Filter Incremental Adaptive Unsharp Sharpen [^]
M
Incremental Adaptive Unsharp Sharpen [^]
M
Do a small incremental sharpen on the image using the 'adaptive unsharp sharpen' method:
New image = Original image + Convolve(original image, kernel) where kernel =
![$ \frac{1}{16}\times\left[ \begin{array}{ccc}
-1 & -2 & -1 \\
-2 & 12 & -2 \\
-1 & -2 & -1 \end{array} \right]$](img15.gif)
Filter Sharpen By... [Ctrl+6]
M
Sharpen By... [Ctrl+6]
M
Sharpen an image by a specified amount using one of 5 convolution kernels.

Filter Laplacian of Gaussian...
M
Laplacian of Gaussian...
M
Alternative sharpening filter. The Gaussian operation smoothes noise. The Laplacian part enhances
edges by both down-weighting and up-weighting the opposing values across an edge. The image is
filtered by a LoG filter and the result is added to the original image to produce the sharpening.
Filter X Derivative
M
X Derivative
M
Computes the local gradient in the X direction based on the x-1,x+1 values.
Filter Y Derivative
M
Y Derivative
M
Computes the local gradient in the Y direction based on the y-1,y+1 values.
Filter Gradient
M
Gradient
M
Filter the image according to
Filter Corner Detect
M
Corner Detect
M
A simple corner detection filter which convolves the image with the ![$ \left[ \begin{array}{ccccc}
-1 & -1 & 0 & 1 & 1 \\
-1 & -1 & 0 & 1 & 1 \\
0 ...
...& 0 & 0 & 0 \\
1 & 1 & 0 & -1 & -1 \\
1 & 1 & 0 & -1 & -1 \end{array} \right]$](img17.gif)
Filter Edge Detectors
Edge Detectors Gradient Based...
M
Gradient Based...
M
A simple edge detector which produces a binary image depicting edges according to the
chosen threshold value. The filter simply does a 'Gradient' filter (10.36)
operation and then sets pixels above the threshold value to white, otherwise to black.
Filter Edge Detectors
Edge Detectors Laplacian of Gaussian Based...
M
Laplacian of Gaussian Based...
M
Alternative edge detector based on 'Laplacian of Gaussian' filter (10.33). The
LoG filter produces an image where values across an edge are positive on one side and
negative on the other. The filter then simply computes the zero-crossing points and sets those
with sufficiently high gradient to white, otherwise to black.
Filter Calculate Normals
M
Calculate Normals
M
Computes a field of surface normals from the input image assuming that the input image represents a point cloud
of values in x,y,z so that x = r, y = g, z = b. The normals are then computed based on the neighboring 'x,y,z'
values.
Filter Interpolate Bayer Pattern...
M
Interpolate Bayer Pattern...
M
Interpolate RAW digital camera single channel image into 3 channel image.
Most common high-end digital camera sensors record an image under a color filter array of red, green and blue filters in one of 4 possible arrangements called a Bayer pattern. The filter pattern is a mosaic of 50% green, 25% blue and 25% red. Uninterpolated RAW images are thus single channel, but can be interpolated to 3 channels using the known Bayer pattern.
Possible Bayer patterns:
- RGGB
- BGGR
- GRBG
- GBRG
- Adaptive Homogeneity Directed (AHD):
A relatively new technique which constructs a homogeneity map of the image and uses that map to choose which direction to interpolate in. This significantly reduces color artifacts compared to other techniques. - Second-Order Gradient:
Evaluates gradients around the pixel of interest and makes a smoothness estimate based on the lower of these gradients. Suffers from color artifacts. Recommended to use AHD above
Filter DCT (Discrete Cosine Transform)
M
DCT (Discrete Cosine Transform)
M
Convert an image from the spatial domain into the frequency domain
Filter IDCT (Inverse Discrete Cosine Transform)
M
IDCT (Inverse Discrete Cosine Transform)
M
Convert an image from the frequency domain into the spatial domain
Warp Correct Lens Distortion
M
Correct Lens Distortion
M
'Undistort' the image using the given optical calibration parameters.
Correct Lens Distortion dialog:
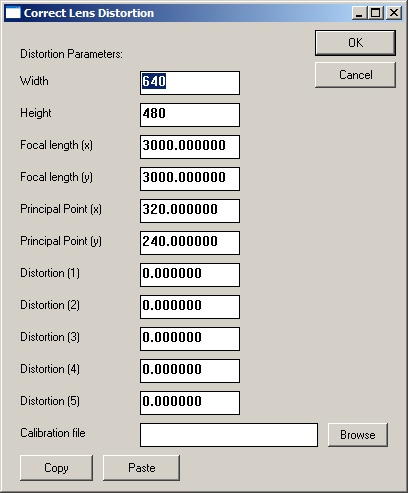
Description of distortion parameters:
- Width: input image width
- Height: input image height
- Focal length (x): focal length of the lens in pixels
- Focal length (y): focal length of the lens in pixels
- Principal Point (x): point through which the Center of Projection passes (usually the center of the image)
- Principal Point (y): point through which the Center of Projection passes (usually the center of the image)
- Distortion (1): Radial distortion
- Distortion (2): Radial distortion
- Distortion (3): Radial distortion
- Distortion (4): Tangential distortion
- Distortion (5): Tangential distortion
kc = [
fc = [
cc = [
nx =
ny =
Where:
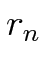 = radial distortion parameters
= radial distortion parameters
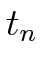 = tangential distortion parameters
= tangential distortion parameters
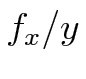 = focal length x/y
= focal length x/y
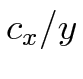 = principal point x/y
= principal point x/y
Effects Vignette...
M
Vignette...
M
Darkens image close to the edges based on the radius value entered in the dialog box.
Used for generating an 'old-fashioned movie camera' appearance.
Effects Randomize
M
Randomize
M
Set the image pixel channels to have random values between 0 and 1.
Effects Sepia tone...
M
Sepia tone...
M
Apply a color tone to a black-and-white version of the image. A color-picker dialog is displayed and
the user chooses the tone. The single channel intensity 10.62 version of the image is then computed
and the pixels values are multiplied by the chosen tone.
Effects Quantize
M
Quantize
M
Rescale the image into the specified number of discrete values.
Effects Signed Quantize
M
Signed Quantize
M
Rescale the image into the specified number of discrete values allowing for negative values.
Effects Vertical Cosine Falloff
M
Vertical Cosine Falloff
M
Applies a cosine scale to each pixel based on the pixel's vertical location. This is used
to scale an image into an equal-area weighted representation. eg lat-long images generated in HDRShop
like some World Map projections, are stretched at the poles (top & bottom) so that those pixels
are over-represented relative to those at the equator (mid-horizontal line of pixels).
Pixel Set/Clear...
M
Set/Clear...
M
Set the pixel channel values within the selected region to the values specified in the dialog.
Pixel Offset...
M
Offset...
M
Increment/decrement the pixel channel values within the selected region by the values specified in the dialog.
Pixel Scale...
M
Scale...
M
Multiply the pixel channel values within the selected region by the values specified in the dialog.
Pixel Divide...
M
Divide...
M
Divide the pixel channel values within the selected region by the values specified in the dialog.
Pixel Power...
M
Power...
M
Raise to a power the pixel channel values within the selected region by the values specified in the dialog.
Pixel Exponentiate...
M
Exponentiate...
M
Raise the values specified in the dialog to the power of the pixel channel values within the selected region.
Pixel Log...
M
Log...
M
Take the Logarithm of the pixel channel values within the selected region in the base of the values specified in the dialog.
Pixel Replace Infinite/NAN...
M
Replace Infinite/NAN...
M
Replace any non-real values with a real value within the selected region.
Pixel Round
M
Round
M
Replace values greater than or equal to 0.5 with 1, and values less than 0.5 with 0 within the selected region.
Pixel Floor
M
Floor
M
Round the channel values down to the next lower integer value within the selected region. eg
Pixel Ceiling
M
Ceiling
M
Round the channel values up to the next higher integer value within the selected region. eg
Pixel Desaturate
M
Desaturate
M
Desaturate the selected pixel values according to the weighting scheme in
http://www.sgi.com/misc/grafica/matrix/.
The weights used are:
D = 0.3086  red + 0.6094
red + 0.6094  green + 0.0820
green + 0.0820  blue
blue
Note that these values are distinct from computing 'Intensity' used elsewhere in the software, which we take as being:
I = 0.299  red + 0.587
red + 0.587  green + 0.114
green + 0.114  blue
blue
Pixel Scale to Current Exposure [Ctrl+0]
M
Scale to Current Exposure [Ctrl+0]
M
Set the channel values to the exposure in the current display within the selected region. Every +1 stop will
double the channel value.
Pixel Clamp at Current Exposure
M
Clamp at Current Exposure
M
Set the channel values to the exposure in the current display within the selected region. Every +1 stop will
double the channel value. Set new channel values of greater than 1 to 1 and divide all channel values by
Used to show the effect of losing some of the dynamic range in an HDRShop image.
Pixel Normalize
M
Normalize
M
Normalize per pixel channels. eg
red channel =
Pixel Lower Threshold...
M
Lower Threshold...
M
Set pixel values of less than the chosen thresholds (per channel) to the threshold values within the selected region.
Pixel Upper Threshold...
M
Upper Threshold...
M
Set pixel values of greater than the chosen thresholds (per channel) to the threshold values within the selected region.
Pixel Swap Byte Order [B]
M
Swap Byte Order [B]
M
Swap the byte order in the case that the current image was created on a system with a different byte order regime.
Pixel White-Balance Selection
M
White-Balance Selection
M
Leverage an area known to be white or gray in the image to color balance the rest of the image. This is useful
where one or more of the channels in the image are overly high.
Procedure: Select an area known or assumed to be any shade of gray up to white and select this menu item. HDR Shop computes the mean channel values within the selected region, takes the intensity (10.62) of the mean values and divides the intensity by the mean channel value, then multiplies each channel in the whole image by the result of that division for that channel. When this is applied, the average channel values in the selected region will now be almost identical (ie gray-white) and this correctional scaling will have been propagated to the rest of the image.
Pixel Scale Selection to White
M
Scale Selection to White
M
Leverage an area known to be white in the image to color balance the rest of the image. This is useful
where one or more of the channels in the image are overly high.
Procedure: Select an area known or assumed to be white and select this menu item. HDR Shop computes the mean channel values within the selected region then each channel in the whole image is scaled by the reciprocal corresponding mean channel value. When this is applied, the average channel values in the selected region will be almost exactly 1 and this correctional scaling will have been propagated to the rest of the image.
Pixel Compute Color Matrix...
Compute Color Matrix...
Compute the
Procedure:
Requires 2 images of the same size to operate on. Select the source and target images from the dialog and click OK. HDR Shop solves by creating a system of linear equations from each pixel channel. This system is then solved by finding the pseudo-inverse using SVD. the resulting
See this tutorial for more information.
Pixel Apply Color Matrix...
M
Apply Color Matrix...
M
Change the pixel values in the image via a
See this tutorial for more information.
Pixel Rasterize Triangle
M
Rasterize Triangle
M
the user specifies a triangle in three points using the point editor (15.12).
Triangle is textured using barycentric coordinates with R, G, B at vertices.
Pixel Index Map
M
Index Map
M
Stores the image pixel coordinates in the red and green channels.
Info Max/Min/Average [I]
Max/Min/Average [I]
Show Maximum/Minimum/Average/Sum/RMS error information about the selected area. Note: if no area is selected,
information for the whole image is shown. Average channel values are the mean. Pixel channel values can be
copied to the text buffer. Pixel locations for maximum and minimum channels are shown beneath the values.
Info Copy Average [C]
Copy Average [C]
Copy the mean channel values within the selected region to the text buffer.
Info Sample Grid...
Sample Grid...
This function is used to create a grid sampling of colors which represent the mean values within the image
or selected area. Typically this is used to color balance an image against a reference set of known colors
such as a Gretag-Macbeth color chart.
Procedure:
There are 2 available methods for obtaining the sample area:
Pre-rectify method:
If the image of the color chart was not orthogonal to the camera you can rectify the chart as a rectangle by first selecting the 4 grid corner points. Mark the 4 corners (Shift+left-click) in a counter-clockwise pattern starting with the top-left corner.
Drag-select method:
Select the area of the image to be sampled or just leave blank if using the whole image.
Select the Image![]() Info
Info![]() Sample Grid... dialog. Enter the grid dimensions and the
number of samples (horizontally & vertically) to be taken from the center of each grid square. 10 samples
in width and height will cause the
Sample Grid... dialog. Enter the grid dimensions and the
number of samples (horizontally & vertically) to be taken from the center of each grid square. 10 samples
in width and height will cause the
![]() square in the grid square center to be used as the samples.
If you are rectifying the image first, a 'Use points to rectify rectangle first' checkbox will be shown
and checked automatically. On clicking 'OK', an intermediate rectangular image is computed from the
homography between the corresponding sets of corners and this image is then used as the input to the
sampling algorithm.
The mean value for each set of grid square samples is computed and output as an image with one pixel for
each grid square with the value of the mean of the samples within the input grid.
square in the grid square center to be used as the samples.
If you are rectifying the image first, a 'Use points to rectify rectangle first' checkbox will be shown
and checked automatically. On clicking 'OK', an intermediate rectangular image is computed from the
homography between the corresponding sets of corners and this image is then used as the input to the
sampling algorithm.
The mean value for each set of grid square samples is computed and output as an image with one pixel for
each grid square with the value of the mean of the samples within the input grid.
See
this
tutorial for more information.
Crop M
Crop the image to the selected area. Either select an area with a 'left-click and drag' operation or with the 'SelectCalculate
Perform various math operations on between one & four of the currently open images.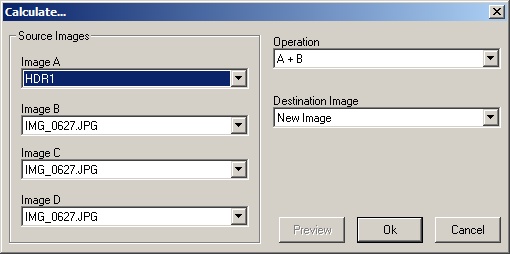
- Addition (A,B) Add A and B
- Subtraction (A,B) Subtract B from A
- Multiplication (A,B) Multiply A and B
- Division (A,B) Divide B by A
- Absolute Magnitude (A) Absolute pixel values in A
-
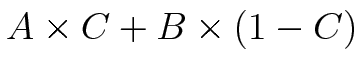 (A,B,C)
Blend A and B weighted by C (alpha blend of B & A with C as the mask)
(A,B,C)
Blend A and B weighted by C (alpha blend of B & A with C as the mask)
- Addition (A,B,C,D) Add A, B, C and D
- Panorama Blend (A,B,C,D) Compute the mean pixel value across all 4 images.
- Maximum (A,B,C,D) Find the maximum values at each pixel in all four images
- Minimum (A,B,C,D) Find the minimum values at each pixel in all four images
- 1 minus image (A) Compute (1 - A)
Duplicate [D]
See 'Window
